.: Filtro de Proyectos :.

Este folleto está dirigido para los niños y las niñas como complemento a los materiales ya existentes en las escuelas. Su contenido ha sido actualizado con el fin de enfatizar el rol que tiene la educación y el proceso de enseñanza aprendizaje en el desarrollo de una cultura de prevención del riesgo en la niñez. Asimismo, se han desarrollado temas relacionados con la importancia de ejercer los derechos de la niñez y –con especial atención- aquella con discapacidad tanto en situaciones de desastre, como en todos los esfuerzos por prevenir el riesgo de desastre. Puede ser útil para estudios sociales, ciencias naturales, estudios relacionados con otros grupos humanos o países, o en la interacción de las personas con su entorno.

https://www.youtube.com/watch?v=TJ_UKn0Y23M

La palabra Xoloitzcuintle, proviene del náhuatl Xólotl que significa dios mexica de la vida y la muerte. Por otro lado, Itzcuintli significa perro.

En la época prehispánica eran sacrificados y enterrados junto con sus dueños pues se creía que tenían el poder de abrir el camino al inframundo.

Se dice que los dioses tenían que descender a Mictlán y obtener un hueso para que se formara la humidad, Xólotl se transformó en perro para tal ofrenda, ahí nació el Xoloitzcuintle. Se adentraba en el peligroso inframundo luchando para renacer en el alba del amanecer, Mictlantecuhtli, el señor de la Muerte le entregó el apreciado hueso, el Xóloitzcuintle regresó al mundo de los vivos y los dioses crearon al primer hombre y mujer.

Estuvo a punto de extinguirse durante la colonización europea ya que se consumía como alimento para resistir las expediciones.

A lo que los muchos de ellos fueron resguardados en la sierra de Oaxaca y Guerrero.

Los perros han sobrevivido más de siete mil años.

13 de septiembre de 1847 - Aniversario 172 de la Batalla de Chapultepec.

Después de la pérdida de Texas y su anexión a Estados Unidos, el presidente James Knox Polk, pide al Congreso de su país que sea declarada la guerra a México, en razón a que, pese a las buenas intenciones de su país, el gobierno mexicano rehúsa, y obra de mala fe cometiendo agravios en contra de su país.

Los problemas iniciaron desde julio de 1845 con la invasión del ejército norteamericano dirigido por el general Zachary Taylor, al terreno en disputa con Texas por los límites territoriales, que tenía su límite en el río Nueces, pero querían que se les reconociera hasta el río Bravo.

Lo anterior aunado a la política expansionista del vecino del norte que quería se le vendieran los territorios de Nuevo México y de la Alta y Baja California, por la cantidad de 15 millones de dólares, que se duplicarían si se permitía el paso libre por el Istmo de Tehuantepec; lo que el gobierno de México no aceptó y consideró que la invasión de las tropas norteamericanas, era una clara provocación; por lo que se dio un enfrentamiento entre ambos bandos el 25 de abril: las del general Taylor y las del general Mariano Arista y, aunque ya se habían dado otros encuentros bélicos, este hecho sirvió de pretexto para que el Congreso de EE.UU. declarara la guerra a México, el 11 de mayo de 1846.

A partir de entonces, el ejército norteamericano, mejor preparado y pertrechado que el mexicano, así como la lenta respuesta del gobierno mexicano que, hasta que el 7 de julio autoriza repeler la agresión, y así lo informó a la población, el presidente interino de México, general Mariano Paredes y Arrillaga: “las agresiones que Estados Unidos de América han iniciado y sostienen contra la República Mexicana, habiendo invadido y hostilizado en varios de los departamentos de su territorio”.

Se sumaron a las agresiones el bloqueo de distintos puertos en el norte del país en ambas costas por la marina estadounidense, que fue obteniendo posiciones hasta lograr su objetivo principal: la Ciudad de México.

Más de un año desde el inicio de la guerra, hasta llegar a la fecha de los hechos nos ocupan, después de un largo camino de derrotas de un país débil y desorganizado, y malas decisiones, como defender Texas, cuando ya estaba perdida, derrota en el Molino del Rey y el que Antonio López de Santa Anna -presidente con licencia-, quien dirigía a las tropas mexicanas, dejara desprotegido el Colegio Militar, ubicado en la parte alta del cerro de Chapultepec; quedando para su defensa unos 800 hombres, muchos de los cuales tenían edades que oscilaban entre los 13 y los 20 años.

Desde el día 12 de septiembre temprano, las baterías americanas hicieron fuego sobre el bosque y el castillo, provocando gran daño a las instalaciones que, de por sí, no estaban muy bien resguardadas pues solo tenían fortificaciones de madera y sacos de tierra, ramajes y adobes; 7 piezas de artillería defendían la posición, los jóvenes cadetes y tropas de indígenas reclutadas de varios estados, sin ninguna preparación, todo esto al mando del general Nicolás Bravo. Retiraron a gran parte de la tropa detrás del cerro para que no sucumbieran ante el nutrido fuego.

El general Bravo pidió inútilmente a Santa Anna que mandara reforzar sus tropas con las reservas pero, por alguna razón, Santa Anna no accedió. Durante la noche se trataron de reparar parte de los daños, pero muchos reclutas indígenas temerosos, aprovecharon la oscuridad para desertar, pues no alcanzaban a comprender la importancia de los hechos.

Nuevamente Bravo, desesperado, solicita el apoyo de Santa Anna, quien con órdenes y contraórdenes traía a la tropa agotada. De último momento, le envía al batallón de San Blas, al mando del coronel Santiago Xicoténcatl. Pero ya era tarde: pues según cuentan las crónicas, a pesar de que el general Bravo les ordenó retirarse, los cadetes del colegio militar decidieron quedarse a defender la plaza y morir con honra. En cuanto tuvieron a su alcance al enemigo, hicieron fuego, pero cuando se les terminó el parque, los sobrevivientes, se reunieron en un jardín donde fueron hechos prisioneros. Los nombres de 6 de los defensores que murieron en aquél día son: teniente Juan de la Barrera, subtenientes Francisco Márquez, Fernando Montes de Oca, Agustín Melgar, Vicente Suárez y Juan Escutia.

La misma suerte corrió el batallón de San Blas que había llegado a auxiliarlos; sucumbe al pie del cerro, casi en su totalidad incluyendo a su jefe Xicoténcatl quien, según el historiador Heriberto Frías “cae el héroe envuelto en su bandera atravesado por veinte balas, gritando ¡Viva México!”.

En la mayoría de los libros de historia, poco o nada se dice sobre la gesta heroica de los cadetes del Colegio Militar. Tampoco en los partes militares de ambos bandos. Se describe la batalla, pero no hay detalles, ni nombres; algunos historiadores, muchos años después, relatan la participación de los seis cadetes antes mencionados en el evento de Chapultepec, de los cuales solo en el caso de Melgar, Montes de Oca y Suárez, hay certeza de su participación; pero, con el transcurso de los años, se fueron agregando elementos ficticios, como que fueron los últimos en morir en la batalla; que terminado el parque lucharon cuerpo a cuerpo y mataron a varios soldados estadounidenses a bayoneta calada. Fueron pereciendo uno a uno hasta que, al ver todo perdido, Juan Escutia, se envuelve en la bandera mexicana para impedir que el enemigo se apropie de ella, muriendo al caer en los riscos al pie del cerro.                                      

En cuanto a las tropas estadounidenses, ya nada los detiene para llegar al “Palacio de los Moctezuma”. Entraron a la Ciudad de México, el 14 de septiembre de 1847, cuyos habitantes los recibieron algunos a pedradas y otros como francotiradores. En cuanto llegaron a Palacio Nacional, cambiaron la bandera del águila y la serpiente, por la de la de las barras y las estrellas.

José María Roa Bárcena y Justo Sierra, entre otros, confieren gran reconocimiento a los Niños héroes por su servicio a la patria.

Para comprender mejor la participación de estos jóvenes del colegio militar en la guerra de intervención de los Estados Unidos de América, analizaremos brevemente los antecedentes que dieron lugar a esta invasión.

En el Castillo de Chapultepec que en 1847 era entonces el Colegio Militar, los soldados y jóvenes cadetes dirigidos por Nicolás Bravo respondieron a los ataques del Ejército de Estados Unidos que !había invadido México! pues quería apoderarse de parte del territorio nacional. Y aunque finalmente fueron derrotados, los niños héroes actuaron como verdaderos hombres, valientes mexicanos dispuestos a dar la vida por su país.

La victoria favorece a los norteamericanos, que obligan a México a suscribir el tratado de Guadalupe-Hidalgo (1848) por el que este último pierde Texas (definitivamente).

Cuentan que cuando todo había acabado un oficial norteamericano observando el rostro de los cadetes muertos, dijo lleno de sorpresa algo como: "¡Pero si son apenas unos niños!", a partir de esta expresión se les llama "Los niños héroes".

Así el 13 de septiembre son recordados todos los héroes que dieron su vida para salvar a la patria durante la guerra contra Estados Unidos.

En la Ciudad de México se realiza un desfile con la armada y en el Colegio Militar se hace una ceremonia con cañones para recordar a los "Niños Héroes". En las demás partes del país se conmemora con ceremonias cívicas.

Después de ser ocupada la Ciudad de México, el 2 de febrero de 1848, en la sacristía de la Basílica de Guadalupe fue firmado el acuerdo con el que se daba fin a la guerra.

En este acuerdo llamado Tratado de Guadalupe Hidalgo, México perdió gran parte de su territorio, reconocía al Río Bravo como el límite entre los dos países y se les daba a los Estados Unidos norteamericanos los territorios de Nuevo México y Alta California.

Por su parte, el gobierno norteamericano entre otros compromisos, tendría que pagar por esos territorios.

A la caída de Tenochtitlán a manos de los españoles, se inicia el proceso de conquista espiritual, económica y social, los habitantes y dueños de todo lo que los recién llegados llamaron “Nueva España” fueron esclavizados y durante 300 años fueron borrados, su cultura y organización social.

En la etapa llamada colonización (a partir del siglo XVI) los españoles se apropiaron de las minas que producían enormes cantidades de metales preciosos como el oro, la plata y otros, agrupados en “encomiendas” los naturales con sus familias fueron asignados como esclavos en las plantaciones, minas y haciendas que sirvieron de premio a los conquistadores que apoyaron a Hernán cortés.

Los criollos hijos de españoles nacidos en Nueva España eran discriminados en los puestos de poder y solo los gachupines como se les llamaba a los españoles nacidos en Europa podían ocupar por designación del virrey o directamente del monarca español.

Como parte fundamental de la conquista los europeos trajeron a sus sacerdotes para imponer su religión, entre los cuales a través del tiempo y de la destrucción y ocultamiento de los grandes centros ceremoniales de la cultura azteca, poco a poco fueron acercando a los “indios” a las iglesias y llegaron a tener un gran poder y riquezas.

Esa influencia y de cierta manera, protección que ejercían los sacerdotes lograron tener una gran influencia entre los esclavos, mestizos y demás grupos que habitaban la Nueva España.

ETAPAS DE LA INDEPENDENCIA DE MÉXICO

Podemos hablar de 3 etapas en el proceso de independencia:

Etapa 1 (1810 a 1814-15): Napoleón Bonaparte gobernaba España a través de su hermano José I. en este periodo en México o la Nueva España, se produjeron grandes revueltas lidereadas por los sacerdotes Miguel Hidalgo y José María Morelos, ambos muertos en las guerras, fue en esta etapa donde se dio el grito de dolores y donde se empezó lo que hoy se conoce como la independencia mexicana.

Etapa 2 (1814 a 1820): este periodo empieza con la expulsión de Napoleón de España por parte de Fernando VII quien vuelve al poder imponiendo un absolutismo ilustrado, anulando la constitución liberal de 1812.

En México o nueva España fue un periodo tranquilo de mucha calma.

Etapa 3 (1820 a 1821): En España hubo un alzamiento liberal por parte de Rafael de Riego que obliga a Fernando VII a jurar la constitución liberal de 1812.

Al conocerse este hecho en la Nueva España, los criollos que nunca habían apoyado a los insurgentes se reúnen y se organizan para conspirar en la independencia de España y evitar caer en las manos liberales. Los criollos que tanto habían defendido el virreinato se juntan con los mestizos e indios para acabar con este.

CONSECUENCIAS DE LA INDEPENDENCIA DE MÉXICO

• La independencia de México fue una gran pérdida para España, principalmente desde el punto de vista económico.
• En México, las élites (comercial y agraria) asumieron el mando político del país, gobernándolo de acuerdo con sus intereses.
• Crisis económica, ya que muchas personas salieron del campo a participar en las guerras lo que llevó a la escasez de mano de obra en el campo que era la principal riqueza de México.
• Crisis Política, cuando la lucha culminó, no había un plan establecido sobre qué sería de México, siendo el país forjado por incesables golpes de estado. Durante los siguientes 30 años, México tendría cerca de 50 gobernantes, resultado de estos golpes militares. Entre 1821-1880, 61 personas tomaron el cargo del país; otras áreas como el ministerio de finanzas fueron dirigidas por 112 líderes entre 1830 y 1863.
• Eliminación de las castas en las clases sociales, las jerarquías en la sociedad acabaron.
• Abolición de la esclavitud, aunque la esclavitud fue abolida en 1829, favoreciendo principalmente a los indígenas y mestizos, poca cosa cambió a las capas más pobres de la sociedad mexicana. Las carencias materiales y la falta de participación política efectiva permanecieron para la gran masa de pobres y miserables mexicanos, que componía la mayoría de la población.

LÍNEA DE TIEMPO O CRONOLOGÍA

1800 – 1810 – Nace la conspiración de Querétaro para levantarse contra el virreinato.

16 de septiembre 1810 – El Padre Miguel Hidalgo anima a los feligreses y da el Grito en Dolores para comenzar con la lucha de independencia mexicana.

1811- En el conocido puente de calderón caen derrotados los indios y los campesinos y apresan a Hidalgo, juzgan, fusilan y decapitan colgando su cabeza en las esquinas de la Alhóndiga de granaditas.

1812 – José María Morelos se hace al frente el mando del ejército independiente y hace su campaña en el Sur del país.

1813 – José María Morelos convoca el primer Congreso Independiente.

1815 – José María Morelos fue derrotado, hecho prisionero y fusilado.

1817 – Francisco Xavier Mina, Mier y Terán, Vicente Guerrero y Torres se alzaron en la lucha por la Independencia.

1821 – Agustín de Iturbide y Vicente Guerrero  promulgaron el Plan de Iguala o de las Tres Garantías, que proclamaba: el cristianismo como una religión única, igualdad o unificación de todos los grupos sociales e independencia mexicana con monarquía constitucional.

Agosto 1821 – Juan de O’Donojú de la nueva España, después México firmó el tratado de Córdoba que ratificaba el Plan de Iguala.

Septiembre 1821 – El ejército Trigarante hace su entrada triunfal a México, y México es proclamado país independiente.

“Defiende tu derecho a pensar,
porque incluso pensar de manera errónea
es mejor que no pensar”

Hipatia
Astrónoma, matemática y filósofa

• Contribuyó a las matemáticas y a la astronomía, siendo maestra filósofa en la biblioteca de Alejandría.
• Fue una de las primeras científicas y matemáticas de la historia.
• Inventó una nueva versión de hidrómetro, instrumento que sirve para pesar líquidos.

Nació en el año 370, en Alejandría, su vida fue un símbolo de la defensa del saber frente a la ignorancia.

Recordarla es un compromiso ya que fue una fuente de conocimiento y educación.

Se dedicó a estudiar las obras más importantes de la Antigüedad, gracias a eso conocemos su trabajo, entre ellos el análisis matemático de los movimientos de los planetas a partir de las tablas astronómicas de Ptolomeo.

Su padre era un famoso filósofo, se aseguró de que creciera con una buena educación y con un gran respeto por su herencia y sus valores griegos, la instruyó en matemáticas y astronomía, proto lo superó y juntos estudiaron astronomía y trabajaron en varias teorías sobre el sistema solar.

Hipatia fue de las últimas representantes de la tradición filosófica en la antigua Alejandría, que fue una ciudad conocida como centro de aprendizaje y conocimientos.

La Biblioteca de Alejandría

Se fundó en el siglo III a.C., siendo la biblioteca más grande del mundo, tenía hasta diez grandes salas para la investigación, cada una dedicada a una disciplina diferente.

Parte de la grabación de un video de la clase cumpliendo una serie de condiciones importantes, como por ejemplo, la duración que no debe exceder de 10 minutos, saber exactamente qué parte de la clase es la que tenemos que poner en esos 10 minutos de video, de manera que ¡no se trata de grabar toda la clase! Sino una parte de la clase que además debe cumplir una serie de condiciones.

En una segunda etapa, (en casa) los alumnos participan e interaccionan  en torno al contenido del video, pero a través de un concepto que se llama Cloud classroom, es decir, que online el alumno debe acceder a las mismas prestaciones que tenía en clase, por eso se pone ese video y se diseña un cuestionario para asegurarnos de que lo ha visto, sin que esto implique una evaluación, sino tener la seguridad de que cada alumno ha visto y participado del video en un foro para intercambiar ideas y aclarar algunas dudas que en el lenguaje común de los niños o jóvenes de la misma edad nos asegurar la comprensión del tema en cuestión.

Ya en el aula se prepara una actividad donde los integrantes del grupo participan de una forma activa, considerando que previamente ha estudiado el tema en el video  ya en este espacio de tiempo nos aseguramos de que los alumnos practiquen y realicen alguna actividad.

Este es el modelo pedagógico que se llama Flip teaching, es decir, “la lección en casa, las tareas y actividades en clase”.

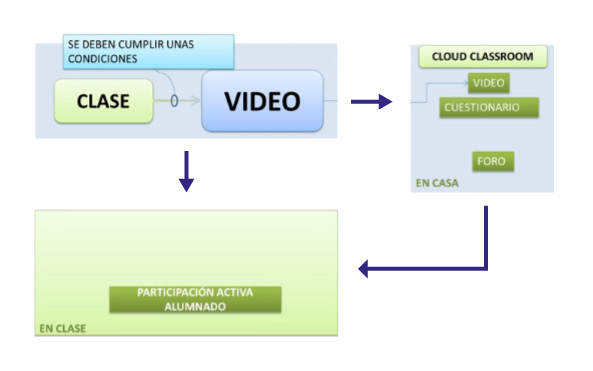
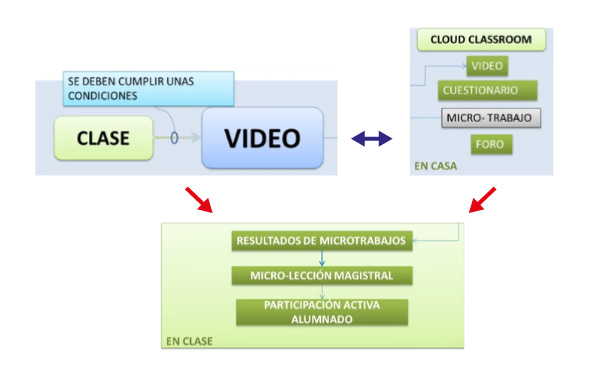
Sin embargo, este modelo es muy general ya que en ocasiones podemos encontrar dificultades para crear el video y las actividades, por esa razón es recomendable adaptarla a un Micro Flip teaching, para hacerlo específico, de una sola clase o un solo contenido de aprendizaje.

La organización consiste en que después de analizar el video, participar en el foro en clase y aclarar las dudas y resolver las interrogantes de manera interactiva, realiza un trabajo específico de la asignatura de que se trata, el contenido de la clase en la parte fundamental que hemos seleccionado para editar el video y en un Micro espacio que facilita el trabajo y evita la saturación, las prisas y exigencias que generan ansiedad en los estudiantes. Así de esta manera, en actividades que hemos llamado Micro Flip teaching, los estudiantes tienen la oportunidad de preguntar, aclarar dudas y de manera activa lograr aprendizajes significativos.

“Dios algunas veces geometriza”, Platón (427-347 a. C.).

Phi (Φ,φ) -el número áureo, de oro o de Fibonacci- es un concepto de sobra conocido y estudiado por matemáticos de todos los tiempos, pero que a su vez, tampoco es del todo ajeno para los amantes del arte, la biología, la arquitectura, la música, la botánica o las finanzas, por ejemplo. No es difícil que se hayan tropezado con él en cualquiera de estas disciplinas. ¿Significa esto que es posible entonces encontrar una traducción numérica para todo lo que vemos, oímos o construimos a nuestro alrededor? Quizás la respuesta más cercana que podamos dar a esta pregunta sea la frase de Platón que abre este artículo.

Sin embargo, sí podemos indagar en un fenómeno matemático que ha atraído la atención de pensadores de todas las disciplinas y épocas desde que fuera descubierto: la proporción áurea o la divina proporción. Para entrar en materia tenemos que remontarnos a la historia del matemático Leornardo Bigollo (Leonardo Pisano o de Pisa), Fibonacci.

LA ESPIRAL DE FIBONACCI

Phi (Φ,φ) se llama Phi gracias al famoso escultor griego Fidias (siglo 5 a. C.), autor de grandes hitos arquitectónicos como el Partenón de Atenas. Según cuenta Mario Livio en su libro “La proporción áurea: La historia de Phi, el número más sorprendente del mundo”, ciertos historiadores sostenían que Fidias habría utilizado con esmero la proporción áurea en sus obras. Fue por eso que el matemático estadounidense Mark Barr decidió honrarle nombrando a Φ con su inicial en griego (Phi). Es decir, Phi, ni fue descubierto por Fibonacci (había sido ya definido y estudiado por Euclides), ni debe su nombre al italiano. Dicho esto, sin embargo, es preciso acudir al hallazgo del italiano para adentrarnos en la potencial capacidad armónica de Phi y sus derivados. La sucesión de Fibonacci y el número de oro son dos caras de la misma moneda.

La sucesión que descubrió el matemático pisano (0,1,1,2,3,5,8,13…) entraría dentro del campo de la aritmética (estudia los números y las operaciones elementales que se pueden realizar con ellos). De esta sucesión deriva el número áureo, representado con la letra griega Phi(Φ,φ) y que sirve para expresar la relación entre dos segmentos de una recta. Es decir, Phi es una construcción geométrica (en relación a las propiedades de las figuras) que surge así:

Phi representado como una línea dividida en dos segmentos a y b, de tal manera que toda la línea (a+b) es al segmento más largo a lo mismo que a es al segmento más corto b φ = (a+b)/ a = a/ b /Imagen: Wikimedia commons

Si nos valemos del álgebra para obtener el valor numérico de Φ, recurrimos a una ecuación por la cual Φ= a/b. Por lo tanto, aplicado esto a la representación gráfica del segmento anterior: cuando dividimos el total  de la longitud del segmento (a+b) entre la parte más larga (a) obtenemos el mismo resultado que al dividir la parte más larga (a) entre la más corta (b). El resultado de esta operación es 1.6180339887… lo que es lo mismo, el número áureo definido por Euclides, “un número infinito e irrepetible” (Mario Livio).

Curiosamente, esta cifra es la misma a la que se aproxima el resultado de dividir cualquiera de los números de la sucesión de Fibonacci entre su antecesor (ejemplo: 5/3= 1.666; 13/8=1.625). Uniendo estos dos aspectos, es decir, representando mediante la geometría el concepto aritmético, surge una imagen clave para entender por qué este artículo puede fascinarte aunque no seas matemático ni hayas terminado de entender el entramado numérico que hay detrás del descubrimiento de Leonardo el Pisano: la espiral de Fibonnaci.

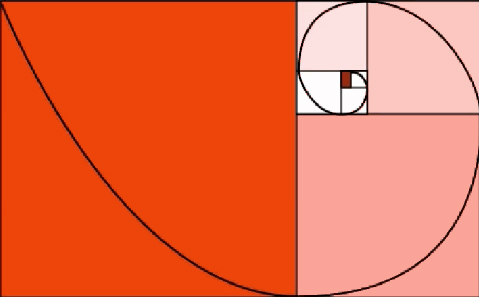
Reproducción del proceso para formar la espiral de Fibonacci en relación a los números que forman la sucesión (longitud de los rectángulos cuya unión da como resultado el trazado de la propia espiral) Imagen: lamentiraestaahifuera.com

UBICUIDAD, ¿CIENCIA O CASUALIDAD?

El número Phi no deja de sorprender con sus propiedades y, al ser descubierto como relación o proporción, ha dado lugar a un amplio análisis de diferentes formas, objetos, representaciones gráficas o incluso patrones de movimiento que tienen lugar en nuestro mundo y que teóricamente están más o menos directamente relacionados con esta proporción, la proporción áurea o divina proporción. El rectángulo áureo o la espiral de Fibonacci, son los ejemplos descritos en este artículo, pero también es posible identificar triángulos áureos o pentágonos áureos. Cualquiera de estas formas se define por tener una propiedad común: respeta la proporción áurea.

Ahora bien, ¿es tan fácil encontrarse con estas formas “áureas” o “divinas” en el entorno que nos rodea? Es decir, más allá de disciplinas como la arquitectura o el diseño, que claramente utilizan las formas y la geometría intencionadamente. ¿Qué pasa con la naturaleza o incluso, con el cosmos? La proporción áurea está en las Pirámides de Egipto, en el logo de Google, en los pétalos de las rosas o en la misma forma de las galaxias. En La Gioconda de Leonardo Da Vinci, en la estructura microscópica de algunos cristales o en las partituras de Debussy. ¿Estamos ante el número más asombroso del mundo? O por el contrario ¿estamos manipulando la realidad queriendo ver matemáticas donde no las hay? Sin duda, después de conocer estos datos tenemos que admitir que las matemáticas tienen una curiosa tendencia a contribuir incluso al conocimiento de materias a las que son, o al menos parecen, totalmente ajenas.

Dory Gascueña para OpenMind

Leonardo Bigollo (Leonardo Pisano o de Pisa) fue un matemático que vivió en Italia entre los siglos 12 y 13 (1170-1240) y que se atrevió a despreciar el sistema de números romanos que imperaba en su época. Ha pasado a la historia con el que fuera su apodo: Fibonacci, un derivado de la suma de los vocablos fillius + bonnacci que en latín e italiano significan algo así como “hijo del bien intencionado”. Al parecer, el padre de Fibonacci (Guglielmo) era buena gente, además de dedicarse al comercio viajando por el norte de África. Fue allí donde su hijo Leonardo descubrió la magia de los números árabes.

Retrato de Fibonacci / Imagen: wikimedia

El sistema indoarábigo viajó desde la India primero a Persia y después a Oriente Medio y el norte de África, desde donde dio el salto a Europa, gracias, entre otros matemáticos, a Fibonacci. El uso de los números árabes que planteaba el pisano incluía la posibilidad de operar con números enteros y fracciones, la división de un número en factores primos, la operación de la raíz cuadrada… No fue fácil adoptar este sistema a pesar de sus numerosas ventajas. Las cruzadas contra el Islam que estaban en marcha por aquel entonces, hacía que cualquier cosa etiquetada como “árabe” quedara automáticamente bajo sospecha. Los números árabes llegaron incluso a ser vetados en la ciudad de Florencia en 1299 con el pretexto de que “eran más fáciles de falsificar que los números romanos”.

Gracias a la actividad comercial de su padre, Fibonacci tuvo la oportunidad de conocer a los grandes matemáticos que había fuera de la burbuja de occidente (Egipto, Siria, Argelia, Grecia…) durante largos viajes a través de diferentes países del mundo árabe y del Mediterráneo. Después regresó a Italia y cuando tenía 32 años publicó el libro Liber abaci (1202), en el que explicaba la importancia del sistema de numeración árabe y lo aplicaba a diferentes situaciones del día a día del mundo del comercio para probar que era más práctico que el sistema de números romanos: el cambio de divisas, la contabilidad comercial, la transformación de pesos y medidas… Un cuarto de siglo más tarde (1227) publicó una segunda edición del mismo libro ampliada y reelaborada que se ha convertido en la versión de referencia de “Liber abaci”, pues actualmente no se conserva ninguno de los ejemplares de aquella primera edición manuscrita de 1202.

Federico II de Hohenstaufen (1194-1250) era el Emperador del Sacro Imperio Romano Germánico cuando conoció el trabajo de Fibonacci gracias a la correspondencia que mantuvo el matemático tras su vuelta a Italia con algunos miembros de su corte, entre los que se encontraba Michael Scotus, astrólogo a quien admiraba el pisano y al que dedicó esa segunda edición de su libro más famoso. Johanes de Palermo(Juan de Palermo) también formaba parte de la Corte y fue él quien retó a Fibonacci con un problema matemático que grabaría su nombre en la historia para siempre.

EL PROBLEMA DE LOS CONEJOS

Un hombre puso un par de conejos en un lugar rodeado por todos lados por una pared. ¿Cuántos pares de conejos pueden ser producidos a partir de ese par en un año si se supone que cada mes, cada pareja engendra un nuevo par que a partir del segundo mes se vuelve productivo?

Un hombre puso un par de conejos en un lugar rodeado por todos lados por una pared. ¿Cuántos pares de conejos pueden ser producidos a partir de ese par en un año si se supone que cada mes, cada pareja engendra un nuevo par que a partir del segundo mes se vuelve productivo?

Fibonacci aceptó el reto y resolvió el problema, publicando la solución en una obra titulada “Flos” (1225). Para ello desarrolló una serie numérica que pasaría a la historia como la serie de Fibonacci.Dicha sucesión de números comienza con 0 y 1, y a partir de ahí cada elemento o número de Fibonacci es la suma de los dos anteriores. Así representó Leonardo el problema reproductivo de los conejos que, aunque es un modelo artificial en el caso de estos animales (pues biológicamente no es estrictamente cierto) sí se cumple a la perfección en el modelo reproductivo de las abejas. En una colmena, sólo se reproduce la reina: es la única que pone huevos.

• Si son fertilizados, surgen las abejas obreras (hembras). Con un 50 % de su carga genética aportada por la madre (reina) y el otro 50 por el padre (zángano).
• Los zánganos o abejas macho se producen a partir de huevos no fertilizados. Así, las abejas obreras hembras tienen dos progenitores y los
• zánganos, uno. El 100% de su información genética es aportada por la madre.

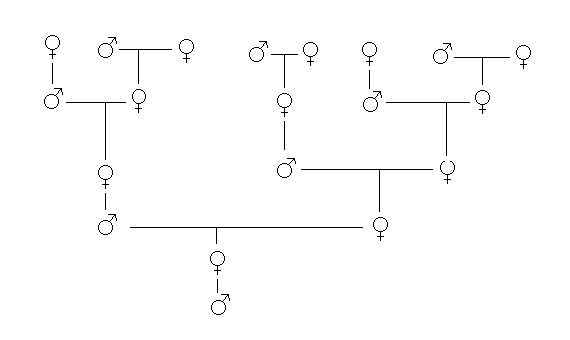
Esquema simulando el árbol genealógico de las abejas / Imagen:Canada’s SchoolNet

Las abejas no son una excepción, pues estos números están detrás de muchos y muy variopintos fenómenos de la naturaleza: la disposición de los pétalos de las flores, la formación de los huracanes… ¿Cómo es posible? ¿Acaso son una combinación mágica, el “abracadabra” de las matemáticas? El misterio detrás de esta sucesión de números que parece estar inscrita en los cimientos matemáticos de todo lo que nos rodea (al menos de muchas de las cosas que existen a nuestro alrededor) fascina a expertos de muchos campos de la ciencia desde hace siglos, llegando incluso a existir publicaciones especializadas en encontrar nuevos campos relacionados con ella.

DE LAS MATEMÁTICAS MEDIEVALES A LA “DIVINA PROPORCIÓN”

Pero, ¿cuánto hay de “magia” en la famosa serie de Fibonacci? ¿Hasta qué punto fue el pisano el descubridor exclusivo de estos números y las proporciones a las que da lugar la relación entre los mismos? La historia ha dejado pistas sobre anteriores menciones de la fórmula, como es el caso de varios matemáticos hindúes: Gopala (1135) y Hemachandra (1150), que ya habían dado cuenta de ella en sus escritos varias décadas antes de la existencia de Fibonacci. Incluso varios siglos después, el mismísimo Kepler (1571-1630) continuó fascinado con la investigación sobre esta serie y desarrolló siglos después el concepto que pasaría a la historia como “la divina proporción”  en su obra “Strena Seu de Nive Sexangula” (1611).

Kepler redescubrió la secuencia a través de la proporción que existía entre los términos consecutivos de la serie.  2 es a 3, lo que 3 es a 5 y lo que 5 es a 8 y así sucesivamente con todos los elementos de la misma. Es decir, existe una proporción (divina proporción o proporción áurea) que se mantiene constantemente al dividir cualquiera de los números entre su predecesor en la serie. Esta proporción se representa con el número phi (en honor al escultor griego Fidias y no a Fibonacci): φ = 1,618.

Kepler ya definió en su obra “Strena Seu de Nive Sexangula” (1611) la importancia de esta proporción, que según él, se desarrollaba de una manera análoga en el proceso reproductivo, consiguiendo así perpetuarse. La idea de Kepler sobre un proceso biológico de autorreplicación marcado por la secuencia de Fibonacci fue ignorada por los biólogos hasta hace relativamente poco, cuando la filotaxis  -disposición de las hojas en un tallo- se consolidó científicamente.

Sea como fuere, el descubrimiento de la serie numérica que dio lugar a la divina proporción le valió a Fibonacci la permanencia en el tiempo y en la memoria de las matemáticas. En el siglo XIX una estatua en su honor fue erigida en Pisa y a día de hoy puede visitarse en el cementerio de la ciudad, en la Piazza dei Miracoli. No hay muchos datos sobre el final de su vida, aunque sí existe un decreto por el cual la República de Pisa concede un salario vitalicio a Leonardo pisano en 1240 en reconocimiento por su servicio a la ciudad como consejero en materias de contabilidad.

Dory Gascueña